퍼셉트론의 활성화 함수(계단 함수), 신경망의 활성화 함수(시그모이드 함수)
대표적인 활성화 함수를 이용해 두 함수를 비교 해봅시다.
파이썬을 이용해 각 함수를 구현하면서 비교하겠습니다.
계단 함수
계단 함수는 0보다 크면 1 아니면 모두 0을 출력하는 함수입니다.
def step_function(x):
if x > 0:
return 1
else:
return 0위 코드는 넘파이를 적용할 수 없어 아래 코드를 사용합니다.
def step_function(x):
y = x > 0 #bool 형태로 저장
return y.astype(np.int) #int로 형변환 해주면서 true=1, false=0
step_function(np.array([1.0, 2.1, -1.1])) #array([1, 1, 0])
계단 함수를 그래프로 나타내 보면
import numpy as np
import matplotlib.pylab as plt
def step_function(x):
return np.array(x>0, dtype=np.int) #위 함수를 더 줄인 것
x = np.arange(-5.0, 5.0, 0.1) #-0.5~0.5 까지 0.1 간격으로 넘파이 배열 생성
y = step_function(x)
plt.plot(x,y)
plt.ylim(-0.1, 1.1) #y축의 범위 지정
plt.show()
계단 모양처럼 생겨서 계단 함수입니다.
이제 시그모이드 함수를 살펴봅시다.
시그모이드 함수를 식으로 먼저 보면

시그모이드 함수는 계단 함수와 달리 특정 값을 출력합니다.
어떻게 나오는지 코드를 통해 봅시다.
def sigmoid(x):
return 1 / (1 + np.exp(-x))
x = np.array([-0.1, 1.0, 2.0])
sigmoid(x) #array([0.47502081, 0.73105858, 0.88079708])0~1 사이의 값으로 출력됩니다.
그래프를 그려 봅시다.
def sigmoid(x):
return 1 / (1 + np.exp(-x))
x = np.arange(-5.0, 5.0, 0.1)
y = sigmoid(x)
plt.plot(x, y)
plt.ylim(-0.1, 1.1)
plt.show()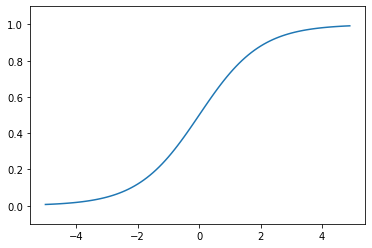
계단 함수와 시그모이드 함수의 그래프를 보면 차이가 잘 보입니다.

시그모이드 함수는 "연속적"으로 값이 변화하고,
계단 함수는 0을 경계로 출력 값이 갑자기 바뀝니다.
이 차이는 즉
퍼셉트론에서는 0 혹은 1이 흐르지만
신경망에서는 연속적인 실수가 흐른다는 뜻이 됩니다.
그럼 공통점으로는 둘 다 입력이 작을 땐 0에 가깝고(혹은 0), 입력이 클 땐 1에 가깝습니다(혹은 1).
입력 값에 얼마냐가 상관없이 0~1 사이의 값을 출력한다는 점이 공통점이 됩니다.
또한 두 함수는 비선형 함수입니다.
두 함수 모두 직선이 아니어 비선형 함수로 분류됩니다.
(비선형 함수 : 직선 1개로 그릴 수 없는 함수)
신경망에서는 비선형 함수를 활성화 함수로 사용해야 합니다.
이유는 선형 함수는 신경망의 층을 깊게 하는 의미가 없어지기 때문입니다.
예를 들어 선형 함수 h(x) = cx를 3층으로 이용한다면
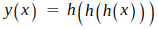
가 되죠 ? 그러면
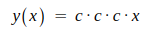
인데 곱셈을 3번 수행하지만

똑같은 식이 됩니다. 이처럼 층을 구성하는 의미가 없어집니다.
마지막으로 ReLU 함수를 살펴봅시다.
시그모이드 함수는 오래전부터 이용해봤으나 최근에는 렐루 함수를 주로 이용합니다.
그래프를 보면 쉽게 알 수 있습니다.
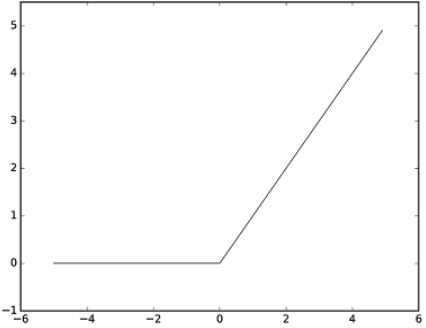
렐루 함수는 0을 넘으면 그대로 출력하고 0 이하면 0을 출력하는 함수입니다.
식으로는
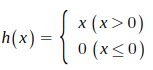
코드는
def relu(x):
return np.maximum(0, x)
# maximum은 두 입력중 큰 값을 선택해 반환하는 함수입니다.
'AI' 카테고리의 다른 글
| 신경망이란 (0) | 2023.10.10 |
|---|---|
| 퍼셉트론의 한계 (1) | 2023.10.10 |
| 단순 논리 회로 (1) | 2023.10.10 |
| [인공지능 학습 HUB] (0) | 2023.10.10 |
| GridSearch - 교차 검증과 최적의 하이퍼 파리미터 찾기 (0) | 2022.12.04 |